Только сейчас поняла, что во время егэ по информатике время на написание кода к каждому заданию будет ограничено. Поэтому сегодня – решение двух предыдущих задач не только без подсказок, но еще и быстро.

Итак, сначала – задание 17 по информатике на последовательность. Заодно закрою прошлые файлы, что бы не подглядывать в код.

В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, разность которых четна и хотя бы одно из чисел делится на 31, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.

Опять “порядок не важен”, т.е. будет два вложенных цикла. Ок, поехали.

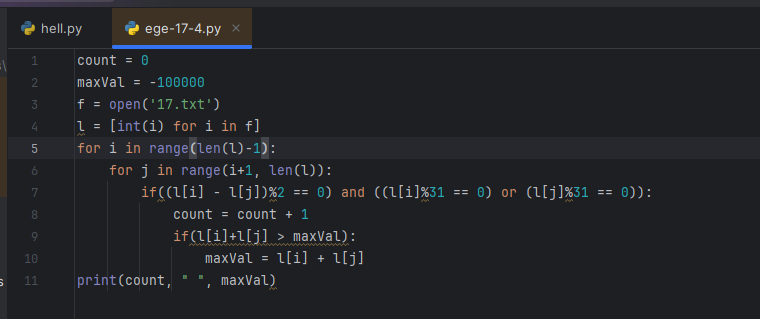
11 строк кода за примерно 10 минут ((( Протупила: еле вспомнила, как перекинуть содержимое файла в массив; синтаксис for – нужно было соображать, что внешний цикл идет до len(l)-1, а внутренний – от i+1. А, ну и новый файл создался не в той директории, поэтому входной файл с данными не нашелся. Быстро сообразила, File – Save As там, где нужно и вперед. Вложенное условие написалось довольно быстро, какое-то типовое оно.

Ок, теперь на рекурсию.

Алгоритм вычисления значения функции F(n), где n  — целое неотрицательное число, задан следующими соотношениями:

F(n) = 0, при n ≤ 1;

F(n) = F(n − 1) + 3n², если n > 1 и при этом нечётно;

F(n) = n / 2 + F(n − 1) + 2, если n > 1 и при этом чётно.

Чему равно значение функции F(49)? В ответе запишите только целое число.

Засад не видится, одна функция с тремя return и вызвать ее один-единственный раз.

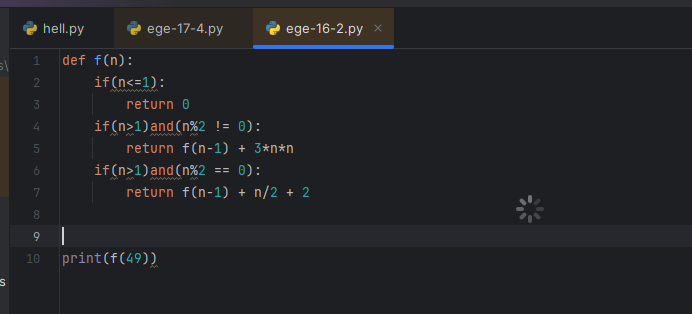
10 строк за примерно 5 минут. Уже норм. о это было задание 16 из егэ по информатике, которое, типа, “Рекурсивные функции с возвращаемым значением”. Значит, пора переходить к следующей разновидности – “Алгоритмы, опирающиеся на несколько предыдущих значений”, это уже День третий. Снова рекурсия