Время идет, поэтому сегодня быстро-быстро прорешиваем задание на последовательность (очень уж там корявый синтаксис по получению массива из файла) и переходим к заданию 23 про Исполнителя, от которого вчера в голове осело до обидного мало. Не переключайтесь.

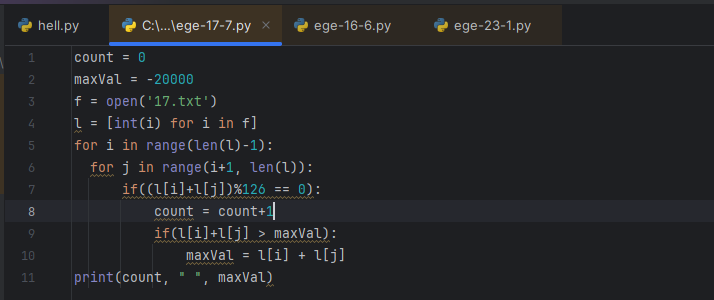
В файле содержится последовательность из 10 000 целых положительных чисел. Каждое число не превышает 10 000. Определите и запишите в ответе сначала количество пар элементов последовательности, у которых сумма элементов кратна 126, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два различных элемента последовательности. Порядок элементов в паре не важен.

Примерно 10 минут, без багов:

Задание 23 по информатике, вспоминаем как решить:

Исполнитель А17 преобразует число на экране.

У исполнителя есть три команды, которым присвоены номера:

1.  Прибавить 1

2.  Умножить на 2

3.  Умножить на 3

Первая команда увеличивает число на экране на 1, вторая – умножает его на 2, третья – умножает на 3.

Программа для исполнителя А17 – это последовательность команд.

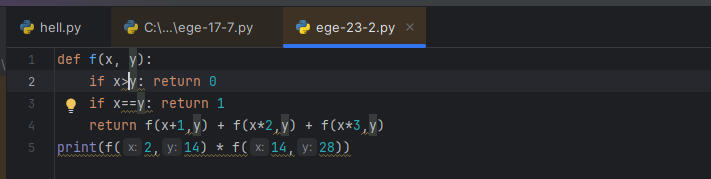
Сколько существует программ, для которых при исходном числе 2 результатом является число 28 и при этом траектория вычислений содержит число 14?

Вспоминаю: функция с x и y, в ней пара левых return’ов с 0 и 1, и один осмысленный, возвращает сумму. Потом двойной ее вызов с перемножением. Поехали.

Примерно 5 минут, без багов. В этом исполнителе же было несколько вариация, а я разбирала только один. Печалька, но придется посмотреть и другие. Начнем с “избегаемым этапом”.

Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:

1. прибавь 1

2. сделай нечётное

Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ – это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 27, причём траектория вычислений не содержит число 26?

Так, с первой частью все понятно – будет функция с x и y, которая в последнем return модифицирует x двумя способами. А вот как посчитать “сколько существует..”, если у нас “траектория вычислений не содержит“? По ходу, самый простой вариант, это вставить в условие для return 0 историю про то, что x = 26. Т.е. просто не подсчитывать траекторию для 26. Пробуем.

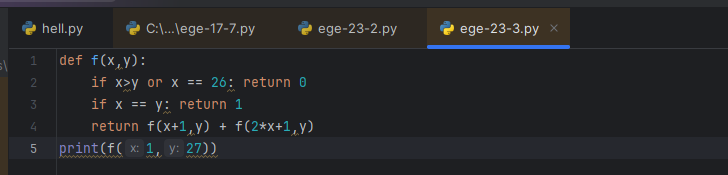
ну да, все на раз-два, только запомнить, что для “избегания” добавляем избегаемое число в условие return 0.

И еще одна вариация – “Количество программ с обязательным и избегаемым этапами”. Выглядит, как комбинация двух предыдущих. Т.е. в функции будет доп.условия на избегаемый вариант, а в результате – будет произведение двух вызовов. “Я так думаю” (с). Ну, посмотрим.

Исполнитель Фибо преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1.  Прибавить 1

2.  Прибавить 2

Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2.

Программа для исполнителя Фибо  — это последовательность команд.

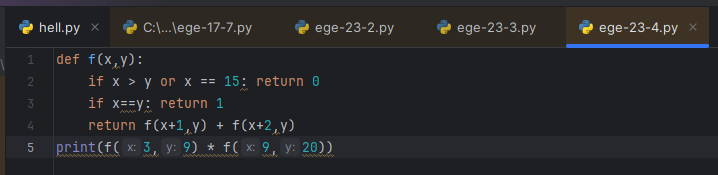
Сколько существует программ, которые преобразуют исходное число 3 в число 20 и при этом траектория вычислений содержит число 9 и не содержит числа 15?

Накидываем код, запускаем, хвалим себя.

Пожалуй, на сегодня все, лень победила необходимость рассмотреть еще одну вариацию задания 23 по информатике. Завтра, все завтра. Тем более, что завтра будет День шестой. Не умеешь сам — научи другого