Быстро пробежим по зубодробительной таблице истинности и пойдем заниматься действительно важными делами. Например, страдать фигней. Итак…
Логическая функция F задаётся выражением (x ≡ ( w ∨ y)) ∨ ((w → z ) ∧ (y → w)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция ??? ??? ??? ??? F 1 1 0 1 0 1 1 0 В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы
А здесь уже зачем-то четыре переменных, придется писать четыре цикла. Функция опять равна 0 в таблице, так что внутри if первым делом будет not. Погнали.
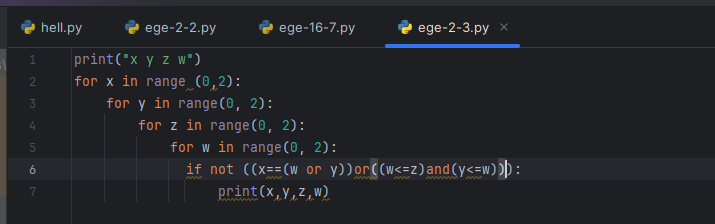
Пришлось изрядно потупить над внутренним if и не поскупиться на скобочки, но все получилось. На выходе вот такое:
x y z w
0 0 0 1
0 1 0 0
0 1 0 1
0 1 1 0
Сравниваем с исходной таблицей и ничего не понимаем (( Так, стоп, в исходной в первом столбце есть 2 единицы. Значит первая переменная – w. Ну или w четвертая, тоже подходит (( А если по строкам? Первая и третья строки могут соответствовать либо набору (0, 1, 0, 1), либо набору (0, 1, 1, 0), и там и там 1ка в y, т.е y-первая переменная. z равно 1ке только в одном получившемся наборе, т.е z-в третьем столбце. w-тогда 4ая. А для x остается только второе место. Т.е. yxzw. Тот самый случай, когда мало код написать, дольше приходится результаты разбирать, чем писать.