Итак, продолжаем. Сегодня – тип 15 заданий ЕГЭ по информатике, побитовая конъюнкция. Лучше не думать, что значат эти слова, а сразу решать.

Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n.

Так, например, 14 & 5 = 1110₂ & 0101₂ = 0100₂ = 4. Для какого наименьшего неотрицательного целого числа А формула

x & 29 ≠ 0 → (x & 17 = 0 → x & А ≠ 0)

тождественно истинна (т. е. принимает значение 1 при любом неотрицательном целом значении переменной x)?

Похоже на то, что самый простой способ здесь – это способ перебора. Нам нужно найти “наименьшее неотрицательное А”, т.е. первый цикл будет по А от 0 до… ну, до пока не надоест. Внутри будет цикл по х, тоже от 0 до фиг знает скольки. Внутри цикла придется написать if со страшным условием, и если это условие выполнится (станет 1) при всех-всех x, то мы нашли и x, и А.

Погнали. Для начала как-то так:

for A in range(0,1000):
    flag = True
    for x in range (1000):
        f = (x & 29 != 0) <= ((x & 17 == 0) <= (x & A != 0))

Что тут есть? Внешний цикл, на каждом его проходе переменной присваиваем True, мы же оптимисты. Внутри еще один цикл со страшным условием внутри (хорошо, что в Питоне есть оператор <= , который соответствует стрелочке в задании, все равно не помню. как эта фигня называется). Дальше надо думать, что буду делать потом, пока можно просто запустить и посмотреть на тормознутость питона. А, не, отбежал быстренько, за пару секунд.

Так, в условии “формула … принимает значение 1”. То есть, как эта страшная фигня станет вдруг 0, из внутреннего цикла можно выходить, сбросив флаг в False, фокус не удался и пора смотреть следующее А. Как-то так:

        if not(f):
            flag = False
            break

А вот если после внутреннего цикла наш флаг все еще True, то фокус удался: печатаем текущее А и выходим нафиг и из внешнего цикла:

    if flag:
        print(A)
        break

Дописываем код, запускаем… Да, напечаталось вменяемое значение А = 12. Проверяем, все верно! Итого:

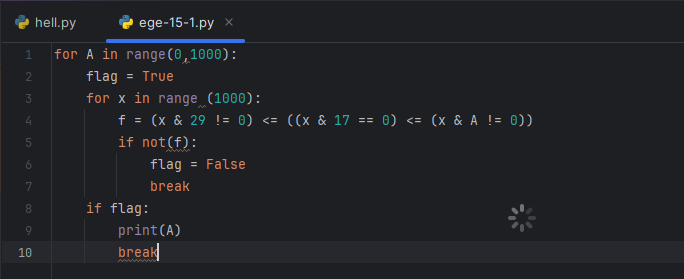
Ну вот и все, первый пример из типа (или варианта?) 15 ЕГЭ по информатике оказался не таким страшным, как его название. Главное – не запутаться в скобочках при написании формулы для f