Итак, снова тип 15 задания ЕГЭ по информатике, на этот раз – координатная плоскость. Страшновато, но делать нечего ((

Сколько существует целых значений числа A, при которых формула

((x < 5) → (x² < A)) ∧ ((y² ≤ A) → (y ≤ 5))

тождественно истинна при любых целых неотрицательных x и y?

Что б я так жил, как я это знаю. Придется думать ((

Напрашивается самый внешний цикл по А, внутри него будет счетчик. Счетчик будем наращивать, если формула “тождественно истинна при любых х и у”. Значит, еще два вложенных цикла по х и у, и если при любой их комбинации формула истинна, пора наращивать счетчик. Я так думаю (с).

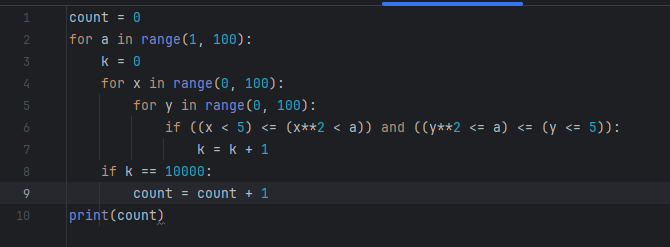
Вот такая вот получилась конструкция. Во внутренних циклах бегу по х и у, считаю функцию; если она True, наращиваю k. Ну а если пробежав 100*100 раз в этой несчастной k лежит 10000, то функция при любой перебранной комбинации х и у была True, пора наращивать счетчик count.