Итак, впереди ждут “Алгоритмы, опирающиеся на несколько предыдущих значений”. Звучит слегонца стремно, но пути назад нет.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(2) = 3

F(n) = F(n–1) * n + F(n–2) * (n – 1) , при n >2

Чему равно значение функции F(5)?

Вообще непонятно, почему это должно как-то отличаться от обычной задачи на рекурсии. Одна функция, в ней три return, вызвать ее при одном значении. Ок, нефиг тут думать, трясти надо.

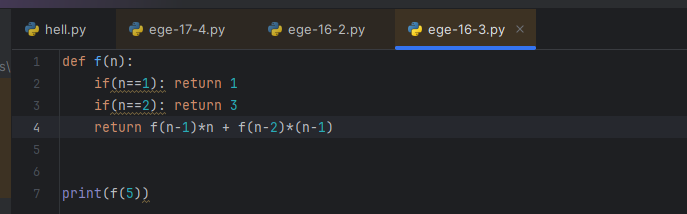
Получилось как-то совсем изи. В функции третий if писать не стала, сразу return, скорость написания кода при решении заданий егэ по информатике важнее его чистоты, сорян. Для закрепления – еще один вариантик.

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 5;F(2) = 5;

F(n) = 5*F(n − 1) − 4*F(n − 2) при n >2.

Чему равно значение функции F(13)? В ответе запишите только натуральное число.

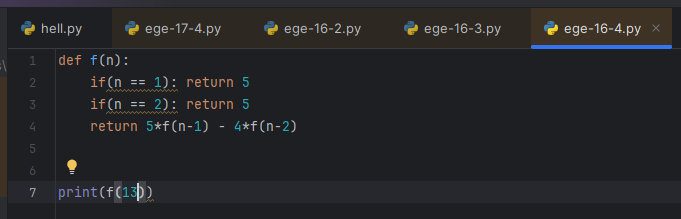
Ок, хватит на сегодня этой фигни, посмотрим, чем кормят в теме “Алгоритмы, опирающиеся на одно предыдущее значение”. Например

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1

F(n) = F(n–1) * n, при n >1

Чему равно значение функции F(5)

Ну, ок, на раз-два.

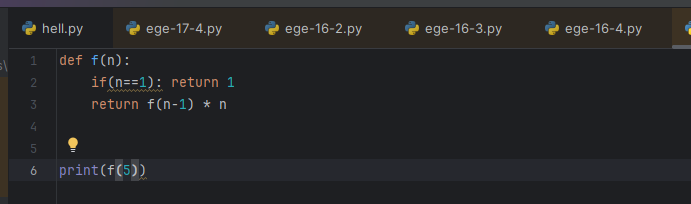
Так, хватит на сегодня, вообще не интересно так. А завтра будет День четвертый. Следуй за белым кроликом